Heap 너란 아이는...
대충격적 사실
자료구조에서 Heap과 메모리에서 Heap은 완전 다른 의미다.
이걸 알게된 건 바야흐로 백준 최소힙 문제를 풀던 도중 알게됐다.
일단 처음엔 문제에 주어진 조건을 구현해서 아래 코드로 제출했다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import sys
n = int(sys.stdin.readline().rstrip())
heap = []
zero_cnt = 0
res = []
for _ in range (n):
x = int(sys.stdin.readline().rstrip())
if x > 0:
heap.append(x)
elif x == 0:
if len(heap) > 0:
res.append(heap.pop(heap.index(min(heap))))
else:
res.append(0)
zero_cnt += 1
for i in range (zero_cnt):
print(res[i])
흠 근데 이렇게 풀면 pop을 할 때마다 min index를 구해야되는데 이걸 n번 반복하니 총 O(N^2)의 시간 복잡도가 걸린다.
리스트 요소가 100,000개 이하까지 주어질 수 있다고 했으니, 최악의 경우엔 백억번(ㄷㄷ)이 걸릴 수 있다는거다.
따라서 저 코드를 제출하면 3%까지 계산하다 곧바로 시간초과가 뜬다.
그래서 deque로 풀어보려했는데, 가만 생각하니 deque의 popleft 메서드엔 argement가 들어가면 안돼서 sorting을 해야되는데 그러면 입력 받을 때마다 정렬하는거니 이것도 비효율적인데…
그래서 으뜩하지? 하는 중,
파이썬 라이브러리 중에 heapq라는게 있다고 해서 ㅇㅎ 그럼 이걸로 풀면 되겠구나 하고 문제를 풀었다.
따라서 정답 코드는 아래와 같다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
import sys
import heapq
n = int(sys.stdin.readline().rstrip())
heap = []
zero_cnt = 0
res = []
for _ in range (n):
x = int(sys.stdin.readline().rstrip())
if x > 0:
heapq.heappush(heap, x)
elif x == 0:
if len(heap) > 0:
res.append(heapq.heappop(heap))
else:
res.append(0)
zero_cnt += 1
for i in range (zero_cnt):
print(res[i])
heapq 라이브러리는 최소힙을 구현한 것이다. 그 중 heappop 메서드는 해당 트리에서 가장 작은 요소를 빼내는 메서드이며 시간복잡도는 O(log N)이 걸린다.
고로 위 코드에서 총 시간 복잡도는 O(N log N)이 되고 최악의 경우엔 약 170만번이 걸린다는거다.
백억번과 170만번의 차이는 가히, 말할 수 없다.
그렇담 왜 Heap에서의 pop은 O(log N)의 시간이 걸리며, 애초에 이 문제를 왜 틀렸을까? Heap을 잘 모르기 때문이다.
고로 Heap의 개념을 차근차근 살펴보자.
자료구조에서 Heap이란,
자료구조에서 Heap이란 우선순위 큐(큐가 데이터를 FIFO로 빼내는데 이 특징을 무시하고, 특정 우선순위를 정해서 데이터를 빼낸다는거다)의 구현을 위해 만들어진 완전이진트리 형태의 자료구조다.
우선순위큐는 추상적인 자료형(ADT)이고, Heap은 이를 구현하는 구체적인 자료구조다. 그래서 우선순위큐를 구현하는데에는 다른 방식들도 있지만, 그 중 Heap이 다른 방법들보다 가장 효율적이고 널리 사용되는 방법인 것이다.
이 때 우선순위큐에서 주로 사용되는 특정 우선순위는 최소 또는 최댓값이다. 그래서 Heap의 종류에도 최소/최대힙이 있는거다.
이 때 Heap은 완전이진트리형태인데, 기존의 완전이진트리와 다른 점은 노드에 중복값이 존재할 수 있다는 점이다.
참고로 완전이진트리라는것은 트리에서 맨 마지막 레벨을 제외하고는 모든 레벨의 노드가 완전히 꽉 차있다는걸 말한다.
따라서 Heap에서 데이터를 삭제할 때는 루트노드 그니까 맨 위에 있는 노드를 먼저 삭제하는데, 최소힙일 경우 루트 노드는 해당 이진트리 안에서 가장 작은 값일테니까 얘를 search하는건 O(1)의 시간이 걸리는거다.
그리고 얘를 빼내는건 루트 노드를 제거하고 트리의 마지막 노드를 루트로 옮긴 후 트리가 힙 속성을 만족하도록 “힙화” (heapify)하는 작업이 필요한데, 이를 만족시키기 위해서는 트리의 깊이에 비례하는 최대 log N번의 비교와 교환이 필요하다.
따라서 삭제(heappop) 연산은 O(log N) = O(1) * O(log N)의 시간복잡도를 갖는 것이다.
근데 도중에 드는 생각이 동적 객체는 메모리 힙에 쌓이지 않는가. 스택 메모리와 자료구조 스택은 의미적으로 관련이 있으니, 메모리 힙이랑 자료구조 힙도 서로 관련이 있나? 하고 찾아봤는데 아니라는거다.
우리 Heap은요…
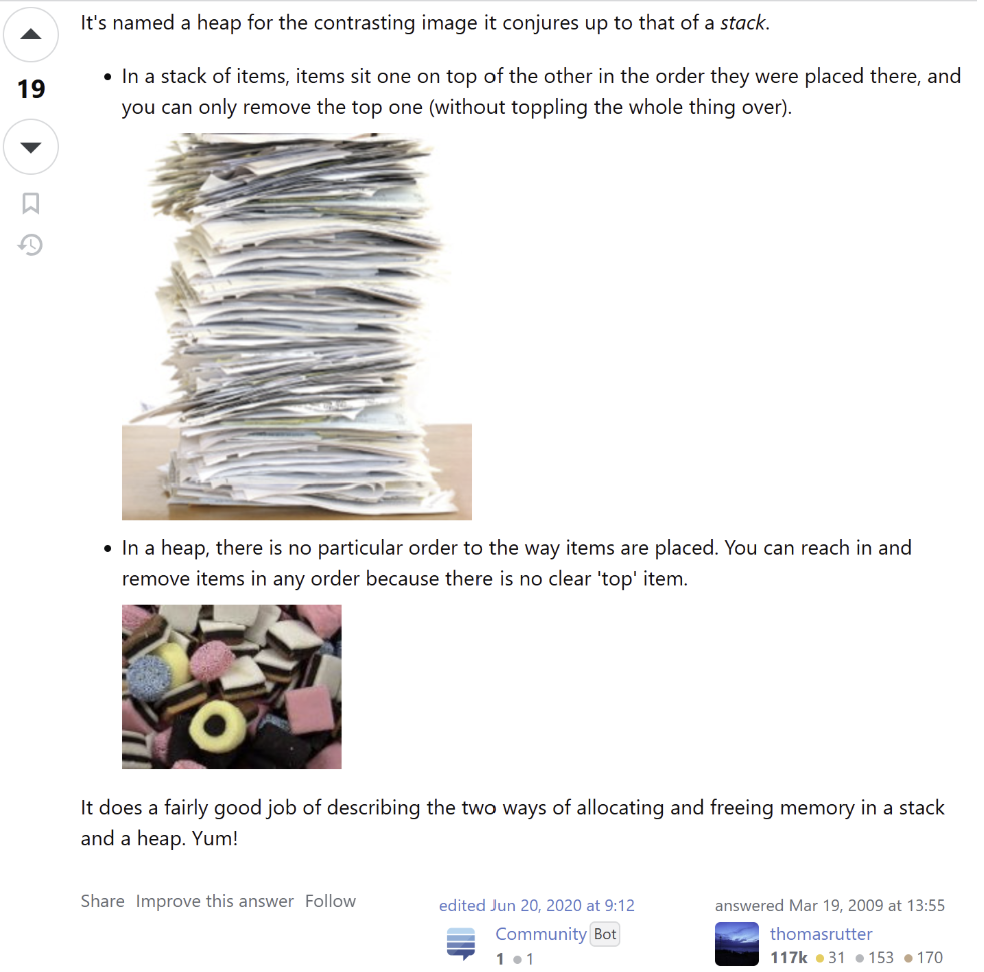
일단 Heap의 사전적 의미는 널부러진 더미들을 밀한다. 마치 정리되지 않고 쌓여있는 빨랫감처럼 말이다.
메모리 Heap은 동적 객체를 할당하는 공간이다. C++ 기준 동적 객체는 HeapAlloc을 활용해서 마음대로 할당하고 해제할 수 있다. 따라서 정해진 순서없이 메모리 블록을 자유롭게 할당하고 해제할 수 있기 때문에 메모리가 마치 더미와 같은 형태를 보인다고 Heap이라고 하는거다.
그럼 자료구조에서는 왜 Heap이라고 부르는걸까? Heap의 사전적 의미가 정리되지 않고 쌓여있는 더미를 말한다고 했지 않는가?
근데 Heap은 루트 노드가 해당 트리의 최소/최대값이니, 어떻게 보면 정리가 되어있다고도 할 수 있는거 아닌가?
응 아니다. 이는 완전 정렬된 구조가 아니라 “부분적”으로만 정렬이 된 상태니까 Heap이라고 할 수 있는거다.
완전정렬된건 AVL 트리에서나 그런거고, Heap은 아니다.
그래서 Heap이라고 부르는거다!ㅅ!
왜, 눈이 eye라는 의미도 갖고 있고, snow의 의미도 가지지 않는가. Heap도 이처럼 그냥 동의어인것이었다. 정말 대충격적 사실 ㅇㅅㅇ
참고 자료