그냥 중위 표기법 쓰면 안되나요?

왜 수식 표기법에는 전위, 중위, 후위가 있을까? 수식 표기법과 이를 코드로 작성하는 방법을 살펴보자.

수식 표기법이 필요한 이유

우리는 일반적으로 수식을 나타낼 때 3 + 4 * 2 와 같이 연산자를 피연산자들 사이에 넣어서 표기한다.

따라서 이러한 표기법을 중위표기법(infix)이라 한다.

근데 컴퓨터 입장에선 중위 표기법을 알아보지 못한다.

우리는 3 + 4 * 2를 보면 그냥 바로

아~ 4 * 2 먼저 하고, 그 값에 +3 하면 되겠네?

라고 생각할 수 있지만, 컴퓨터는 +가 먼전지, *가 먼전지 모른다.

공학용 계산기에서도 그렇고.

그래서 중위표기식을 전위(prefix) 또는 후위(postfix)로 바꿔주는 과정이 필요하다.

근데 여기서 이런 의문을 가질 수도 있다.

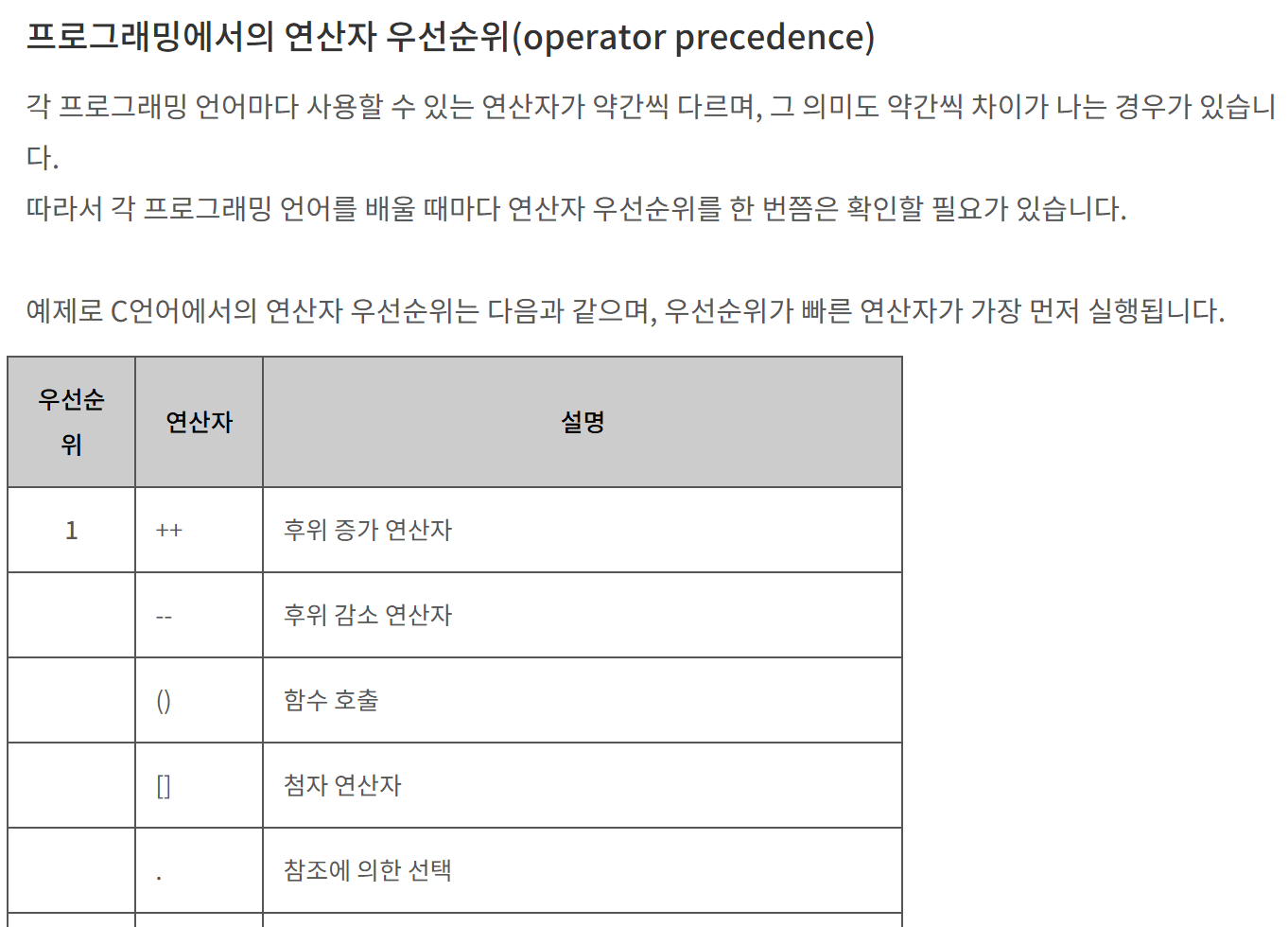
아니, 코드 짤 때 보면 아래 표처럼 연산자 우선순위가 있어서 컴퓨터가 다 알아서 계산해주지 않나요?

그럼 컴퓨터가 중위 표기식을 알아듣는거 아닌가요? 라고 생각하는 당신.

맞다. 우리는 코딩을 할 때 굳이 무슨 전위, 중위, 후위를 따지며 수식을 세울 필요가 없다. 왜? 고급 언어 개발자분들이 그렇게 만들어서 정해줬으니까.

근데 만약 어셈블리(저급언어, 인간말고 컴퓨터에게 친숙한 언어)로 코딩을 하며 수식을 작성해야 된다면?

이렇게 곱셈(IMUL)을 먼저 처리하고 그 후에 더하기(ADD)를 해야한다.

MOV AX, 4
IMUL AX, 2
ADD AX, 3
MOV x, AX

엇, 이렇게 곱셈을 먼저 처리하고 그 후에 더하기를 한 과정.

이 과정 자체가 후위 표기법이다.

그래서 중위 표기법을 후위 표기법으로 바꾸려면 (피연산자1, 피연산자2, 연산자)의 순서대로 적는거다.

따라서 X = C + A * B 를 후위 표기식으로 바꾸면 X C A B * + =이 된다.

전위 표기법은 반대로 (연산자, 피연산자1, 피연산자2)의 순서로 나타내면 된다.

ㅇㅋ 이제 왜 표기법을 적어야되는지 알겠다.

그럼 중위를 후위로 바꾸는 알고리즘은 뭘까?

Shunting Yard Algorithm

1. 피연산자는 바로 출력
2. 연산자는 스택에 push()
   • 단, 스택의 맨 위 연산자의 우선순위가 현재 연산자보다 우선순위가 더 높거나 같으면 스택의 맨 위 연산자를 pop()
3. 왼쪽 괄호는 무조건 스택에 push()
4. 오른쪽 괄호를 만나면 왼쪽 괄호가 나올 때 까지 연산자를 pop()
5. 수식을 다 읽었으면 스택에 남은 연산자 모두 pop()

expression = "3 + 4 * 2 / ( 1 - 5 ) ^ 2 ^ 3"
tokens = expression.split()

output = []
stack = []

# 연산자 우선순위 딕셔너리
precedence = {'+': 1, '-': 1, '*': 2, '/': 2, '^': 3}
# 거듭제곱은 오른쪽 연산자이기에 (e.g 2^(3^2)) 따로 지정
right_associative = {'^'}

for token in tokens:
    if token.isalnum():  # 숫자나 변수는 바로 출력하기 위해 그냥 push
        output.append(token)
    elif token == '(':  # 여는 괄호는 스택에 넣음
        stack.append(token)
    elif token == ')':  # 닫는 괄호면 여는 괄호 나올 때까지 pop
        while stack and stack[-1] != '(':
            output.append(stack.pop())
        stack.pop()  # 여는 괄호 제거
    else:  # 연산자일 때
        while (stack and stack[-1] != '(' and
               (precedence[stack[-1]] > precedence[token] or # 연산자 우선순위가 높거나
               (precedence[stack[-1]] == precedence[token] and token not in right_associative))): # 같으면
            output.append(stack.pop()) # 맨 위에 있는 요소를 빼고
        stack.append(token) # 현재 연산자를 스택에 push

# 남은 연산자 모두 출력
while stack:
    output.append(stack.pop())

# 결과 출력
print(' '.join(output))